一根牙签能“横着”放进一个多小的地方？

“你能在一个任意小的地方，把一根牙签360度地转一圈吗？”

这听起来是不是像魔术？其实，这正是一个叫做挂谷猜想的数学问题！

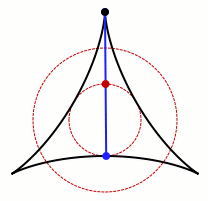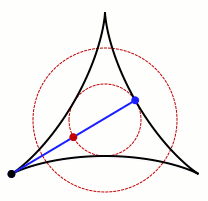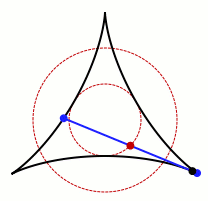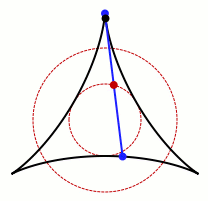
这幅图展示了一个在三尖瓣线的内部旋转的转针。 在它转动的每一阶段（除了一个端点是在三尖瓣线的一个顶点时），转针与三尖瓣线相交于三个点：两个端点（蓝色）和一切点（黑色）。 转针的中点（红色）描绘了一个直径等于转针一半的长度的圆。

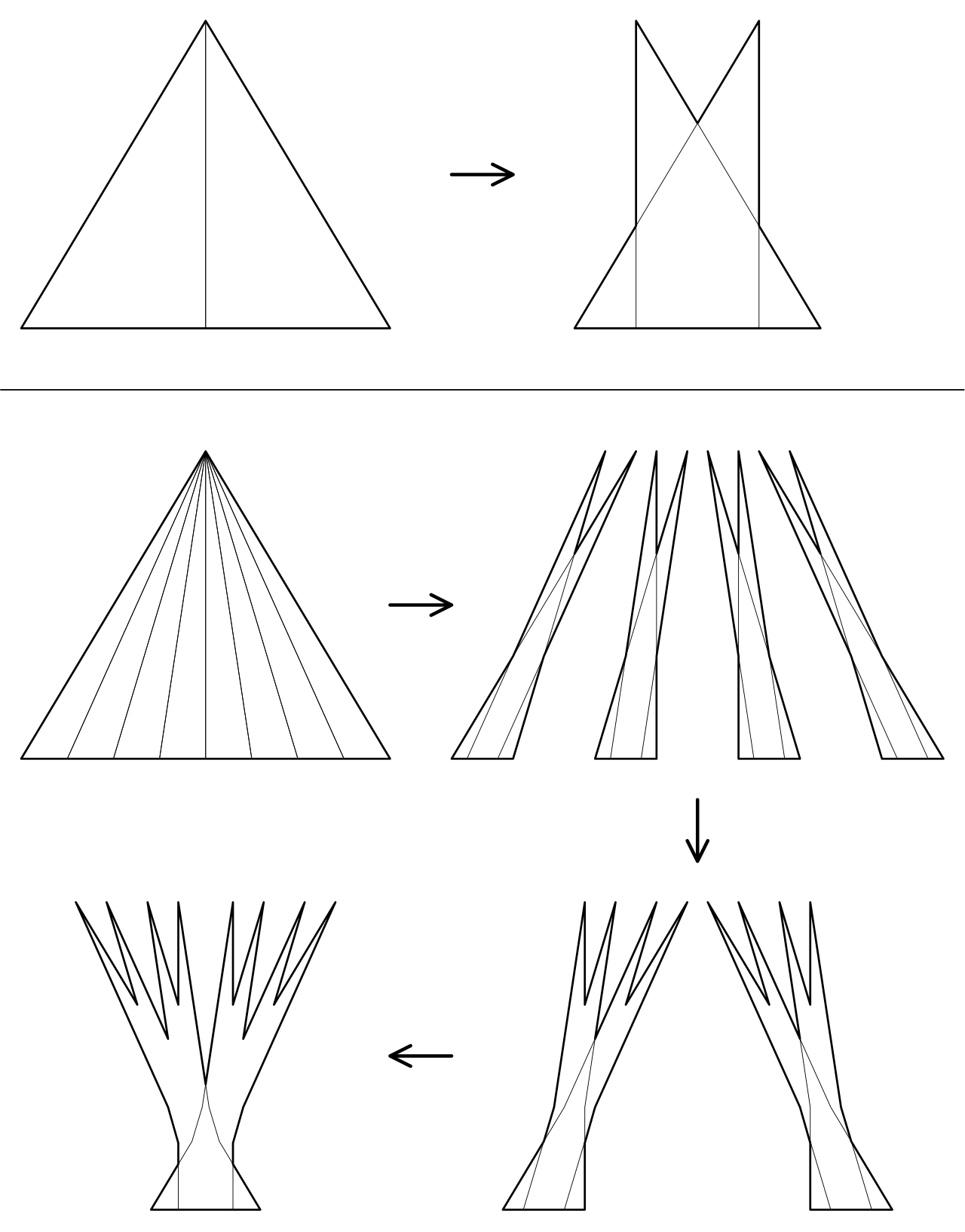
一种“萌芽”方法，用于构造一个小尺度的挂谷集合。这里展示了两种可能的方法来划分我们的三角形并重叠部分以得到一个较小的集合，第一种方法是我们只使用两个三角形，第二种方法是我们使用八个三角形。请注意，与原始起始形状相比，最终形状的大小有多小。

问题的由来

在1917年，日本数学家挂谷宗一（Sōichi Kakeya）提出了一个有趣的问题：

你能在一个尽可能小的面积里，把一根长度为1的针（或线段）转一整圈吗？

这不是“针尖跳舞”的诗意，而是严肃的数学：

我们不是说“针围绕中心转”，而是“任意方向都能出现”，哪怕不在同一个位置。

这个区域现在被称为：

挂谷集（Kakeya set）——一个可以让一根单位长度的线段转向所有方向的集合。

为什么这个问题重要？

虽然看起来像个“几何小游戏”，但挂谷猜想影响非常深远，已经和下面这些前沿领域产生了联系：

• 调和分析
• 偏微分方程（PDE）
• 计算机图形学和成像
• 无线通信中的信号传播

特别是在 调和分析中，解决挂谷猜想的技术帮助推动了其他重大猜想的进展，比如傅里叶变换、波前集估计等。